Numba, um compilador Python de alto desempenho

Luiz Irber

luizirber.org

Por que Python é lento?

Tipagem dinâmica
Lookup de atributos
a[1]
- Mesmo no Numpy

Qual a abordagem atual?

Escrever parte crítica em C/C++/Fortran e encapsular
- SWIG
- ctypes
- Cython
- f2py
- CPython API
Escrever diretamente em Cython
- Depois de aprender os atalhos e detalhes...

Mas... não dá para ser mais fácil?

Objetivos do Numba

Funcionar com CPython (e Numpy, Scipy e todo o stack científico)
Modificações mínimas no código (inferência de tipos)
O programador decidir o que deve ser acelerado ou não
Possibilitar a criação de extensões estáticas (para bibliotecas)
Produzir código tão rápido quanto C (até mesmo Fortran?)
Suportar array-expressions do Numpy e criação de ufuncs
Produzir código para hardware vetorial (GPUs, aceleradoras, many-core)

LLVM

Provê a infraestrutura

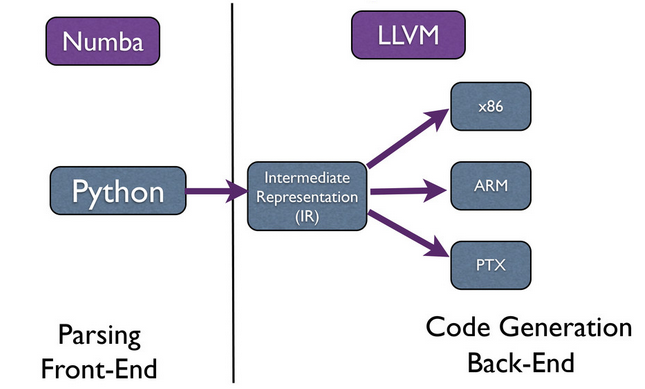
API simples

Dois decoradores:
- jit: programador especifica tipos
- autojit: detecta tipos de entrada, saída, gera código se necessário, e executa

In [1]:

from numba import autojit, jit, double

#@jit('void(double[:,:], double, double)')
@autojit
def numba_update(u, dx2, dy2):
    nx, ny = u.shape
    for i in xrange(1,nx-1):
        for j in xrange(1, ny-1):
            u[i,j] = ((u[i+1,j] + u[i-1,j]) * dy2 +
                      (u[i,j+1] + u[i,j-1]) * dx2) / (2*(dx2+dy2))

Comparando desempenho

http://jakevdp.github.io/blog/2013/06/15/numba-vs-cython-take-2/

"As before, I'll use a pairwise distance function. This will take an array representing M points in N dimensions, and return the M x M matrix of pairwise distances. This is a nice test function for a few reasons. First of all, it's a very clean and well-defined test. Second of all, it illustrates the kind of array-based operation that is common in statistics, datamining, and machine learning. Third, it is a function that results in large memory consumption if the standard numpy broadcasting approach is used (it requires a temporary array containing M * M * N elements), making it a good candidate for an alternate approach."

In [2]:

import numpy as np
X = np.random.random((1000, 3))

Python puro

In [3]:

def pairwise_python(X):
    M = X.shape[0]
    N = X.shape[1]
    D = np.empty((M, M), dtype=np.float)
    for i in range(M):
        for j in range(M):
            d = 0.0
            for k in range(N):
                tmp = X[i, k] - X[j, k]
                d += tmp * tmp
            D[i, j] = np.sqrt(d)
    return D

Numpy com broadcast

In [4]:

def pairwise_numpy(X):
    return np.sqrt(((X[:, None, :] - X) ** 2).sum(-1))

Numba

In [5]:

from numba.decorators import autojit

pairwise_numba = autojit(pairwise_python)

@autojit
def pairwise_numba(X):
    ...

Cython otimizado

In [6]:

%load_ext cythonmagic

In [7]:

%%cython
import numpy as np
cimport cython
from libc.math cimport sqrt

@cython.boundscheck(False)
@cython.wraparound(False)
def pairwise_cython(double[:, ::1] X):
    cdef int M = X.shape[0]
    cdef int N = X.shape[1]
    cdef double tmp, d
    cdef double[:, ::1] D = np.empty((M, M), dtype=np.float64)
    for i in range(M):
        for j in range(M):
            d = 0.0
            for k in range(N):
                tmp = X[i, k] - X[j, k]
                d += tmp * tmp
            D[i, j] = sqrt(d)
    return np.asarray(D)

Fortran (não otimizado!)

In [8]:

%%file pairwise_fort.f

      subroutine pairwise_fort(X,D,m,n)
          integer :: n,m
          double precision, intent(in) :: X(m,n)
          double precision, intent(out) :: D(m,m) 
          integer :: i,j,k
          double precision :: r 
          do i = 1,m 
              do j = 1,m 
                  r = 0
                  do k = 1,n 
                      r = r + (X(i,k) - X(j,k)) * (X(i,k) - X(j,k)) 
                  end do 
                  D(i,j) = sqrt(r) 
              end do 
          end do 
      end subroutine pairwise_fort

Overwriting pairwise_fort.f

In [9]:

# Compile the Fortran with f2py.
# We'll direct the output into /dev/null so it doesn't fill the screen
!f2py -c pairwise_fort.f -m pairwise_fort > /dev/null

In [10]:

from pairwise_fort import pairwise_fort
XF = np.asarray(X, order='F')

Scipy

In [11]:

from scipy.spatial.distance import cdist

Scikit-learn

In [12]:

from sklearn.metrics import euclidean_distances

Medindo tudo!

In [13]:

%%capture timeit_measures
%timeit pairwise_python(X)
%timeit pairwise_numpy(X)
%timeit euclidean_distances(X, X)
%timeit cdist(X, X)
%timeit pairwise_cython(X)
%timeit pairwise_fort(XF)
%timeit pairwise_numba(X)

In [14]:

timeit_measures.show()

1 loops, best of 3: 7.19 s per loop
10 loops, best of 3: 41.7 ms per loop
100 loops, best of 3: 16.4 ms per loop
100 loops, best of 3: 7.77 ms per loop
100 loops, best of 3: 7.36 ms per loop
100 loops, best of 3: 7.77 ms per loop
1 loops, best of 3: 6.86 ms per loop

Massageando os dados

In [15]:

from pint import UnitRegistry
ureg = UnitRegistry()

labels = ['python\nloop', 'numpy\nbroadc.', 'sklearn', 'scipy', 'cython', 'fortran/\nf2py', 'numba']
times = []
for line in timeit_measures.stdout.split('\n')[:-1]:
    value, unit = line.split(':')[-1].split('per')[0].strip().split()
    times.append(ureg.Quantity(float(value), unit).to('seconds'))

measures = list(reversed(sorted(zip(times, labels))))
measures

Out[15]:

[(<Quantity(7.19, 'second')>, 'python\nloop'),
 (<Quantity(0.0417, 'second')>, 'numpy\nbroadc.'),
 (<Quantity(0.0164, 'second')>, 'sklearn'),
 (<Quantity(0.00777, 'second')>, 'scipy'),
 (<Quantity(0.00777, 'second')>, 'fortran/\nf2py'),
 (<Quantity(0.00736, 'second')>, 'cython'),
 (<Quantity(0.00686, 'second')>, 'numba')]

Comparando resultados

In [17]:

labels = [m[1] for m in measures]
timings = [m[0].magnitude for m in measures]
x = np.arange(len(labels))

ax = plt.axes(xticks=x, yscale='log')
ax.bar(x - 0.3, timings, width=0.6, alpha=0.4, bottom=1E-6)
ax.grid()
ax.set_xlim(-0.5, len(labels) - 0.5)
ax.set_ylim(1E-3, 1E2)
ax.xaxis.set_major_formatter(plt.FuncFormatter(lambda i, loc: labels[int(i)]))
ax.set_ylabel('time (s)')
ax.set_title("Pairwise Distance Timings")

Out[17]:

<matplotlib.text.Text at 0x42b6950>

Apresentação executável

https://github.com/luizirber/pythonbrasil9/blob/master/numba.ipynb

Anaconda para dependências
pip install pint

Obrigado

luizirber.org

luiz.irber@gmail.com